摘要: 利用燃料电池流道简化方法和压力速度耦合算法,研究了U形和Z形2种结构的电堆空气分布,以及歧管宽度和燃料电池单体数量对空气分布的影响.结果表明:由于U形和Z形结构的歧管出口压力分布不同,导致2种结构的空气分布不同,Z形结构的空气分布要比U形结构好;歧管尺寸增大时,空气分布的均匀性得到了明显改善,当空气分布差异不大时,再增加歧管尺寸,效果会降低,且增加电堆成本;在电池数量增加、歧管横截面积不变时,空气分布的均匀性会明显变差,尤其是U形结构;当电池数量为30个、歧管宽度为20 mm时,空气分布较均匀;当电池数量为50个时,歧管宽度需要达到30 mm,空气分布才较均匀.
1 数学模型
1.1 变量数和自由度分析
式中:Qin为进口歧管体积流率;qx为燃料电池流道体积流率;pin为进口歧管压力;Δpin为进口歧管内的压降;i为单体燃料电池序号,i=1,2,…,N,N为单体燃料电池数量.
pout(i)=pout(i-1)+Δpout(i),
式中:Qout为出口歧管体积流率;pout为出口歧管压力;Δpout为出口歧管内的压降.
pout(i-1)=pout(i)+Δpout(i).
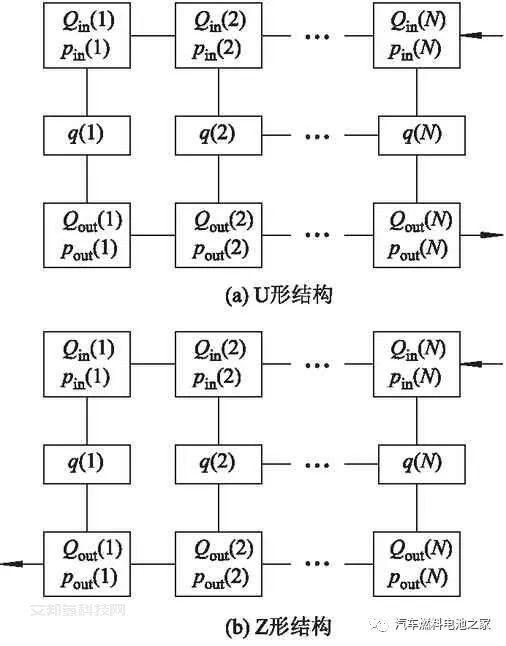
总入口体积流率Qin(N)等于U形结构中的总出口体积流率Qout(N)和Z形结构中的总出口体积流率Qout(1),并且已给出.未知数共有5N个,共有(2N+2)个Qin、Qout、qx相关联的方程,只需要再知道N个qx的方程及(2N-2)个pin、pout和流速方程,模型就可以计算.
1.2 模型假设与边界条件
质子交换膜燃料电池电堆有着复杂的几何结构,并且建立1个完整的模型需要很多的计算资源,因此提出1个简化的模型十分必要.通过设置1个等效阻力系数将各单体燃料电池流道简化成1个直流道,流道与歧管的横截面形状都是正方形,流道的横截面积为1 mm2.等效流动阻力系数可以参考文献[11].
为了简化计算,假设如下: ① 流体为连续不可压,流动为层流;② 不考虑流道中气体的电化学反应消耗;③ 燃料电池流道内的流体流动过程用达西定律来描述;④ 流体流动过程中温度恒定.
式中:I为电流,I=300 A;γ为过量系数,γ=2.5;R为理想气体常数;T为运行温度,T=338.15 K; n为粒子带电数,n=4 个;F为法拉第常数;φ为空气中氧的体积分数,φ=0.21;p为工作压力,p=0.202 MPa;RH为相对湿度,RH=50%; psat为水的饱和蒸汽压.
1.3 压力和流速关系
式中:μ为气体黏度,μ=1.9×10-5 Pa·s-1;vx为燃料电池流道内气体流速;1/K为等效阻力系数,1/K=4×107 m-2;Lx为直流道长度,Lx=0.1 m; Ax为流道横截面积.
式中:ρ为气体密度,ρ=1.24 kg·m-3;vy为电堆歧管内气体流速;g为重力加速度;h为高度; f为摩擦因子;Ly为相邻流道间歧管的距离,Ly=3 mm; Dh为流道的特征长度;Kc为局部阻力系数,Kc=0.5;Q为电堆歧管体积流率;Ay为歧管横截面积.
通常,重力势能项比其他项至少小1个数量级,在这里忽略不计.电堆歧管间的压降为
此时方程的未知数和方程的个数相等,自由度为0,模型已经可以计算.
1.4 压力速度耦合算法
参考文献[12]提出的求解算法,假设总气体流量平均分配到每个燃料电池内.ref为参考电池序号,对于Z形流场,ref=1;对于U形流场,ref=N.燃料电池体积流率、流道内压降及歧管间的体积流率计算方法如下:
对于Z形流场和U形流场来说,根据式(10)歧管的流速和压降的关系以及出口压力设置为0的已知条件,只需要计算出压降就可以知道pin和pout,计算方法如下:
pin(ref)=pout(ref)+Δpx(ref),
将式(18)-(20)代入到式(2)、(4)、(6)中, 可以求得pin和pout.
由于初始假设歧管流体分布均匀,因此定义参数β对qx进行修正.
当β值较大时,这意味着此时燃料电池的体积流率与歧管间的压降不匹配,因此β称为流动分布因子,为了使迭代计算更加准确,需要对初始值进行调整.调整因子为
将调整因子代入到式(14)中得新的参考燃料电池流道压降为
根据得到的新参考压降值,燃料电池进口歧管间的压力随之更新,更新后的进口歧管压力记为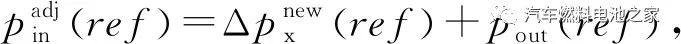 需要注意的是出口压力不用调整,因为出口压力等于0,根据歧管进口压力和出口压力就可以得到新的燃料电池流量分布.计算方法如下:
将残差值的收敛标准设置为1×10-4,如果ERR≥1×10-4,进入下一次迭代,如果ERR<1×10-4,则模型收敛,输出qx(i),计算结束.使用Matlab 2016b对整个算法进行编程求解.
需要注意的是出口压力不用调整,因为出口压力等于0,根据歧管进口压力和出口压力就可以得到新的燃料电池流量分布.计算方法如下:
将残差值的收敛标准设置为1×10-4,如果ERR≥1×10-4,进入下一次迭代,如果ERR<1×10-4,则模型收敛,输出qx(i),计算结束.使用Matlab 2016b对整个算法进行编程求解.
2 结果与讨论
2.1 U形和Z形结构空气体积流率分布
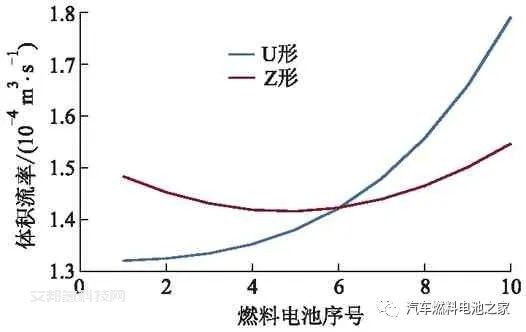
燃料电池空气体积流率变化曲线如图2所示,U形结构和Z形结构的燃料电池空气分布趋势有明显的差别,在单体燃料电池数量为10个、歧管的宽度为6 mm时,Z形结构的电堆空气体积流率分布更均匀,在实际工作中为了方便安装,大多采用U形结构.
2种结构的歧管进、出口压力变化曲线如图3所示,造成2种结构空气体积流率分布趋势不同的主要原因是出口流动方向不同导致歧管出口压力分布不同.
2.2 歧管宽度对空气体积流率的影响
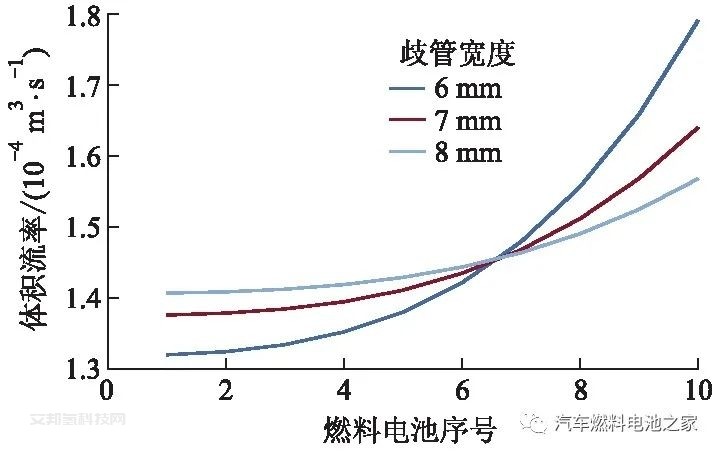
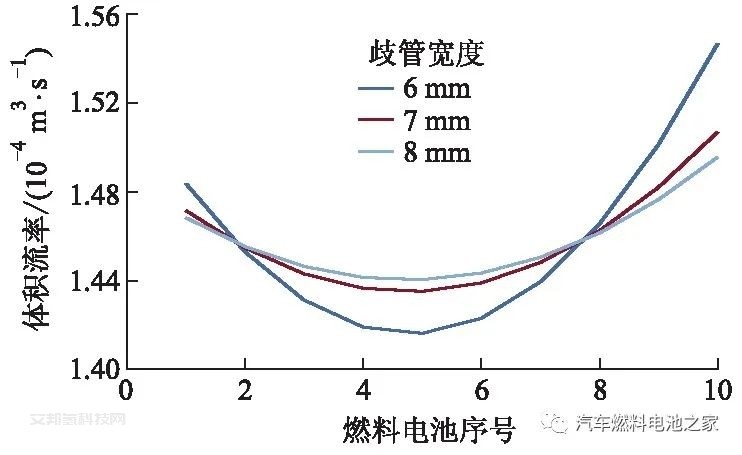
歧管宽度对U形和Z形结构歧管空气体积流率的影响分别如图4、5所示.歧管宽度增大会明显改善空气体积流率分布的均匀性,这是因为空气通过歧管的压降减小,迫使燃料电池的空气分布变得均匀.当歧管宽度由6 mm增加到7 mm时(当歧管横截面的宽度改变时,歧管横截面的长度也做同样改变),空气体积流率分布均匀性得到了较大改善,歧管宽度从7 mm增加到8 mm时,空气体积流率分布的均匀性虽有提升但变化不大.从性能角度分析,歧管的宽度不能过小,但是当空气体积流率分布差异不大时,再增加歧管宽度,效果会降低,且会增加电堆成本.
2.3 单体燃料电池数量对空气体积流率的影响
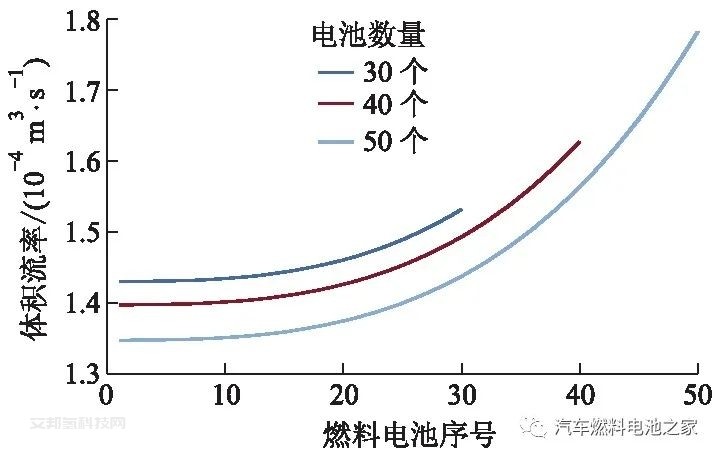
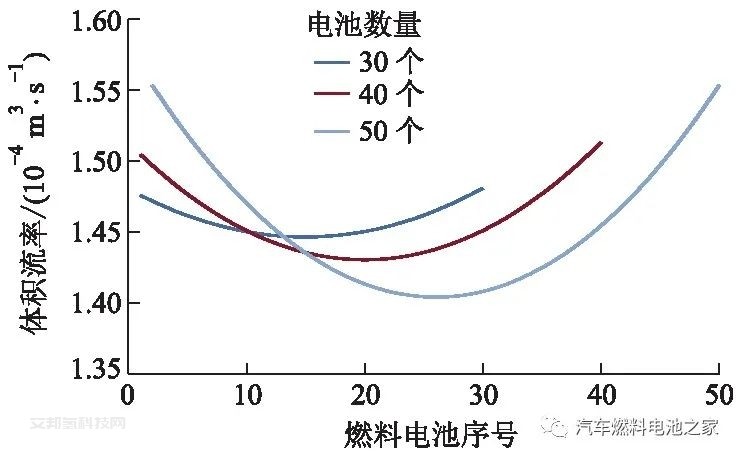
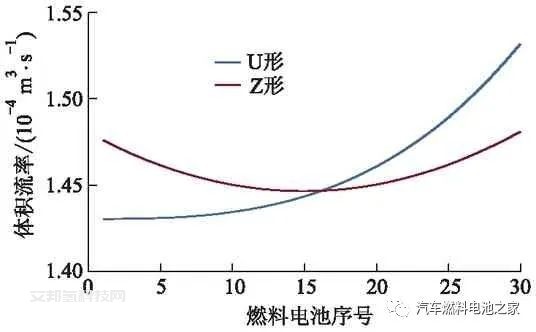
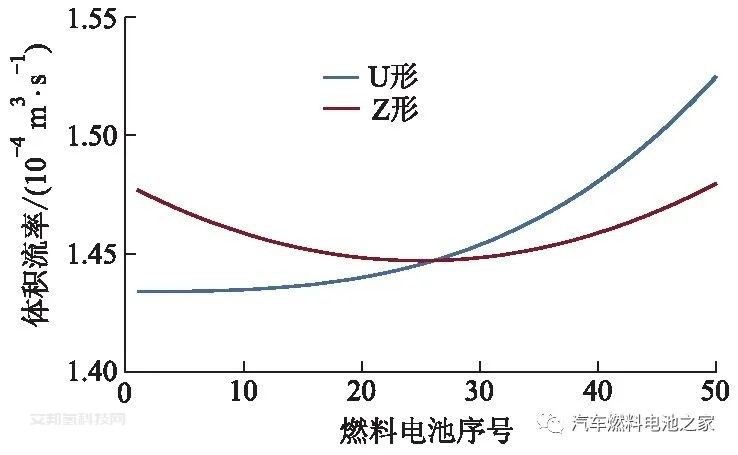
歧管宽度为20 mm,单体燃料电池数量不同时,U形和Z形结构电堆空气体积流率变化曲线分别如图6、7所示.单体燃料电池数量从30个增加到50个,2种结构的空气分布均匀性都开始降低,但U形结构降低得更多,这会严重降低电堆性能,导致输出的平均电压变低,会对燃料电池造成较大损害.
图6 燃料电池单体数量不同时U形结构 电堆空气体积流率变化曲线
图7 单体燃料电池数量不同时Z形结构 电堆空气体积流率变化曲线
歧管宽度为20 mm、单体燃料电池数量为30个时,电堆空气体积流率变化曲线如图8所示.歧管宽度为30 mm、单体燃料电池数量为50个时,电堆空气体积流率变化曲线如图9所示.从图8、9可以看出:当单体燃料电池数量为30个、歧管宽度为20 mm时,空气分配较均匀;电池数量为50个时,歧管宽度需要达到30 mm,空气分配才较均匀.
图8 歧管宽度为20 mm、单体燃料电池数量为 30个时,电堆空气体积流率变化曲线
图9 歧管宽度为30 mm、单体燃料电池数量为 50个时,电堆空气体积流率变化曲线
3 结 论
1) U形结构和Z形结构由于出口方向不同导致歧管出口的压力分布不同,从而使空气分布趋势不一样,Z形结构的空气分布均匀性比U形好.
2) 电堆歧管宽度增大,会明显改善流体分布均匀性,当流体分布差异不大时,再增加歧管宽度,效果会降低,且成本增加.
3) 在电池数量增加,且歧管宽度不变时,空气分布的均匀性会明显变差,尤其是U形结构.当电池数量为30个、歧管宽度为20 mm时,空气分布较均匀,电池数量为50个、歧管宽度需要达到30 mm,空气分布才较均匀.
作者:赵 岩1,2, 罗马吉1,2, 陈 奔1,2
1. 武汉理工大学 现代汽车零部件技术湖北省重点实验室
2. 武汉理工大学 汽车零部件技术湖北省协同创新中心
免责声明:分享此文仅为传播行业相关知识,其版权归原作者所有,感谢原作者的辛苦付出;若有侵权异议等请跟我们联系协商或删除,谢谢!
原文始发于微信公众号(汽车燃料电池之家):基于压力速度耦合算法的PEMFC电堆空气分布
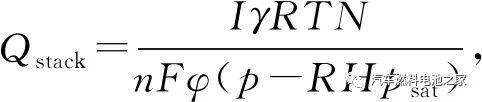
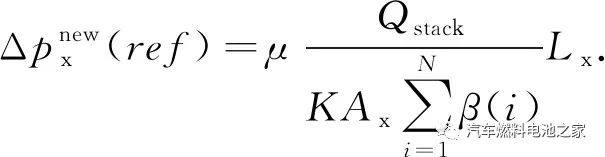

 艾邦氢能产业链通讯录,目前有2200人加入,如亿华通、清极能源、氢蓝时代、雄韬、氢牛、氢璞、爱德曼、氢晨、喜马拉雅、明天氢能、康明斯、新源动力、巴拉德、现代汽车、神力科技、中船712等等,可以按照标签筛选,请点击下方关键词试试
资料下载:
艾邦氢能产业链通讯录,目前有2200人加入,如亿华通、清极能源、氢蓝时代、雄韬、氢牛、氢璞、爱德曼、氢晨、喜马拉雅、明天氢能、康明斯、新源动力、巴拉德、现代汽车、神力科技、中船712等等,可以按照标签筛选,请点击下方关键词试试
资料下载:
 艾邦氢能产业链通讯录,目前有2200人加入,如亿华通、清极能源、氢蓝时代、雄韬、氢牛、氢璞、爱德曼、氢晨、喜马拉雅、明天氢能、康明斯、新源动力、巴拉德、现代汽车、神力科技、中船712等等,可以按照标签筛选,请点击下方关键词试试
资料下载:
艾邦氢能产业链通讯录,目前有2200人加入,如亿华通、清极能源、氢蓝时代、雄韬、氢牛、氢璞、爱德曼、氢晨、喜马拉雅、明天氢能、康明斯、新源动力、巴拉德、现代汽车、神力科技、中船712等等,可以按照标签筛选,请点击下方关键词试试
资料下载:

