电解水中碱性和酸性条件下析氧反应(OER)机理对比

析氧反应（OER）的密度泛函理论（DFT）模拟被认为是理解水分解的局限性必不可少的工具。大多数析氧反应的 DFT 计算都使用酸性反应机制和标准氢电极（SHE）作为参比电极。然而，实验研究通常是在碱性条件下进行的，使用可逆氢电极（RHE）作为参比电极。实验条件和计算条件之间的差异通常通过对后者应用一个与 pH 值相关的校正因子来校正差异。但是，由于酸性和碱性条件下的 OER 反应机理截然不同，因此并不清楚一个简单的校正因子是否能解释这种差异。本文根据碱性反应机理逐步推导出模拟 OER 的理论，并用这一机理解释了以RHE为参比电极的OER过程。这里比较了碱性和酸性 OER 催化机理，并强调了 RHE 和 SHE 的作用。文章详细分析验证了目前文献中的 OER 模拟，并解释了酸性和碱性机理下 OER 计算的差异。

一、简介

析氧反应（OER）通常被认为是水分解的主要瓶颈，因为其动力学过程缓慢，限制了能量转换的效率。在过去的几十年中，人们致力于研究和了解析氧反应。基于密度泛函理论（DFT）计算，人们广泛研究了酸性条件下的 OER 机理。然而，大多数实验研究都是在碱性介质而非酸性介质中完成的。虽然一些计算论文考虑了碱性条件下的 OER 计算，但从反应机理到自由能方程的基础理论并不清晰，也没有明确推导出来。考虑到计算方法与实验方法之间的差异，明确推导出碱性机理下的 OER DFT 计算方程并将结果与酸性机理进行比较至关重要。

被广泛接受的 OER 机制包括酸性和碱性介质中的四个电子/质子转移步骤，如下图1所示。

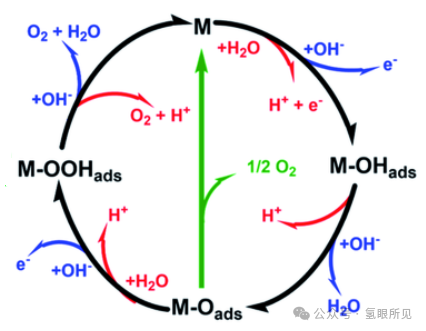
图1：酸性（红色）和碱性（蓝色）条件下的 OER 机制。黑线显示的是通过带有 M-OOHads 中间体的活性位点的 OER 途径。绿色显示的是通过两个 M-Oads 中间体的替代途径。

OER 对 pH 值高度敏感；在酸性条件下，水分子（H₂O）被氧化，释放出（H⁺+ e^-）和氧分子O₂。相反，在碱性条件下，羟基（OH^-）被氧化成 H₂O 和 O₂，同时释放出e^- 。在文献中，许多理论研究在计算典型催化剂（如 Fe₂O₃、Co₃O₄ 和 Ni₃S₂）的 OER 催化活性时都假定了酸性机理。通常以标准氢电极（SHE）为参比电极，通过计算各个反应步骤的吉布斯自由能来表征 OER 的催化活性。

酸性机理涉及到（H⁺+e^-）的产生，其吉布斯自由能通常是通过假设在标准条件（pH=0，压力p_H₂=1bar，T = 298.15 K）下（H⁺+e^-）↔ 1/2 H₂ 的平衡，并使用氢气的吉布斯自由能来隐式计算的。在 pH≠ 0 的条件下，H⁺离子的吉布斯自由能可以通过熵的浓度依赖性 k_BT × pH × ln10 来校正。文献中并未普遍提及这一修正系数的原理和方法，也未明确指出从酸性反应到碱性反应的步骤。

碱性机理涉及OH^- 的氧化，同时释放出e^-。因此，计算 OH^- 和 e^- 的吉布斯自由能对于描述碱性条件下的 OER 至关重要。一些论文声称，OH^- 和 e^- 的吉布斯自由能的计算可以从（H⁺+e^-）的吉布斯自由能中获得，但如何处理 pH ≠0 时（H⁺+e^-）的自由能却没有深入讨论。

利用之前研究所开发的计算氢电极（CHE）方法，以可逆氢电极（RHE）为参比电极，可以正式解决 pH≠ 0 时（H⁺+e^-）自由能的计算问题。此外，与 SHE 相比，RHE 在实验中也通常被用作参比电极。使用 RHE 作为参比电极的主要优点是，在任意 pH 值（压力p_H₂ =1bar 和 T = 298.15 K）下，（H⁺+e^-）的吉布斯自由能等于1/2 H₂ 的能量。

在本文中，从相应的反应和所涉及的物质出发，比较了酸性和碱性条件下的 OER 机理。推导了将 DFT 计算结果与实验相结合所需的理论（但不讨论实际的 DFT 计算）。分别解释了这两种情况下的反应步骤、其吉布斯自由能和过电势。此外，还演示了使用 RHE 和 SHE 参比电极进行的 OER 计算之间的联系，并详细解释了在 pH≠0 的情况下，H⁺离子的吉布斯自由能校正是如何进入能量平衡和过电势的。

二、酸性反应机理下的OER

我们根据OER 的四电子反应机制。在酸性条件下，整个水氧化反应为：

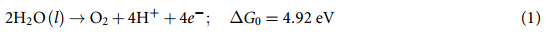
其中 (l ) 指液相。在 p=1 bar 和 T = 298.15 K 条件下，该反应的吉布斯自由能差 ∆G₀ = 4.92 eV。

一般认为该反应分为四个步骤。

其中，^∗代表催化剂的活性位点，(g) 指气相，^∗OH、^∗O 和 ^∗OOH 代表活性位点上吸附的物质（元素）。

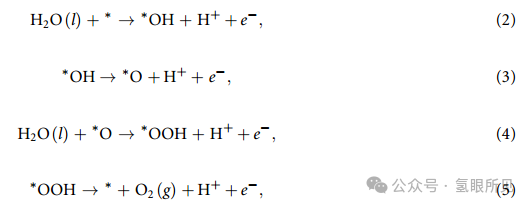
如前所述，在标准条件下，（H⁺+e^-）的吉布斯自由能等于 1/2 H₂ 的吉布斯自由能。反应吉布斯自由能提供了催化剂和 OER 中间产物之间的结合强度，它受到活性位点电子特性的影响。文献中广泛使用的计算反应吉布斯自由能的典型程序是等式 (6)~(9) 所示的在标准条件下与等式 (2)~(5) 相对应的 ∆G^′_n。

其中 E_∗、E_∗OH、E_∗O、E_∗OOH 分别是清洁表面（^∗）和有单一吸附物种 OH、O 和 OOH 的表面的总能量，E_H2O 和 E_O2 分别是 H₂O 和 O₂ 分子的总能量，均通过 DFT 计算获得。∆ZPE 和 ∆S 分别是振动零点能和熵从初始状态到最终状态的变化；T 是温度。此外，∆S 还包含反应 (2)~(5) 中使用的气相和液相的贡献。

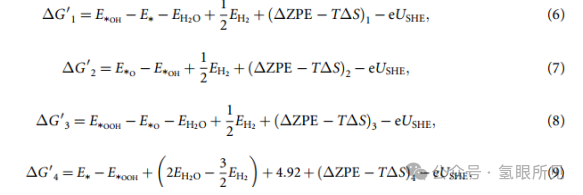
U_SHE 是相对于 SHE 的电极电位。(∆ZPE - T∆S)_n (n = 1, 2, 3, 4) 的计算公式为：

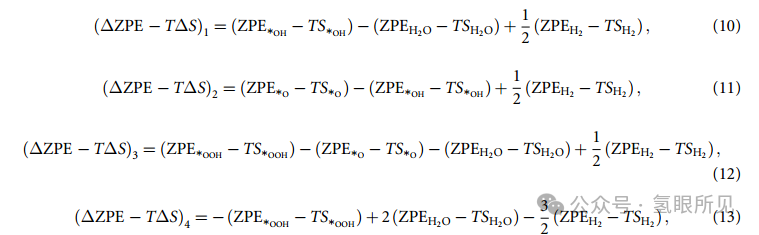
因此，反应周期内 ZPE 项和 TS 项的变化之和等于 0：

等式(6)~(9)的反应吉布斯自由能必须遵循求和规则。

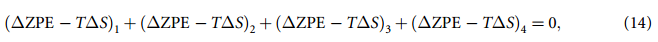
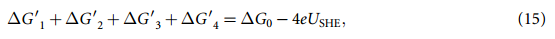
过电势由下式给出：

其中 U₀ = ∆G₀/4e = 1.23 V 是平衡电位，它与 pH 值无关，定义在 p=1bar 和 T=298.15 K 时。任何反应步骤 (2)-(4) 的 ∆G^′_n /e > U₀ 都需要更高的反应电位才能进行，最大 ∆G^′_n /e定义了整个四步反应进行所需的过电位。

三、碱性反应机理下的OER

与酸性条件下的等式(1)不同，碱性条件下的析氧反应由下式（17）给出：

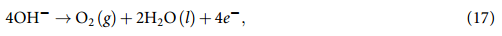
这个反应通常被认为分以下四个基本步骤进行：

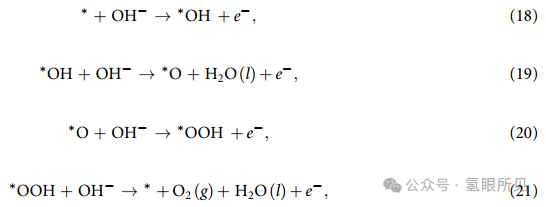
其中的符号与等式 (2)~(5) 中的符号相同。

与酸性机理不同，(18)~(21)式的吉布斯自由能并不常见。因此，我们希望逐步推导出碱性条件下的 OER 机理。等式(18)~(21) 对应的反应吉布斯自由能可表示为：

其中 µ 是所指物质（物种）的（电）化学势。

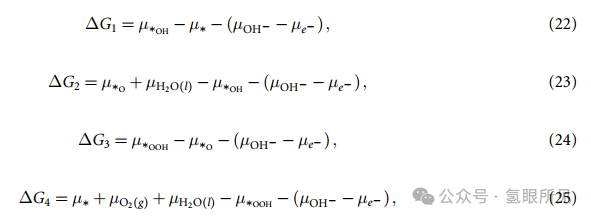
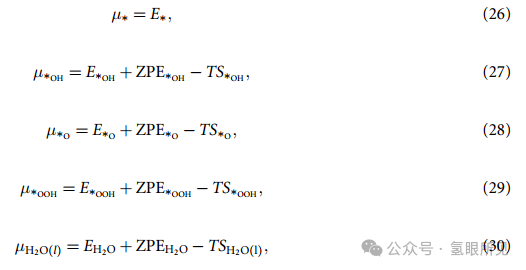
其中，E_∗ 和 E_∗_X 分别是清洁表面 (^∗)和单一吸附物种 X 表面的（DFT）总能量，ZPE_∗X、S_∗X 是相应的振动零点能和熵。E_H2O 是 H₂O 分子的总能量，ZPE_H2O 和 S_H2O_(l)是相应的振动零点能和熵贡献，后者还包含液态的自由能修正。

对于 O₂，由于 DFT 对 O₂ 分子的描述并不完善，因此化学势是根据 O₂ 相对于水的实验形成能得到的。假定平衡为 O₂ (g) + 2H₂ (g) ↔ 2H₂O(l)，则 O₂ 的化学势可写成如下等式。

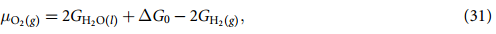
现在，等式(22)~(25) 中剩下的唯一未知数是 µ_OH- 和 µ_e- ，它们分别是 OH^- 和电子（e^-）的化学势，我们实际上只需要( µ_OH^- - µ_e^-) 的差值。为了计算这个差值，我们假定平衡状态为：

化学势的关系如下：

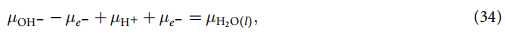
使用小技巧处理如下：

可以改写成如下：

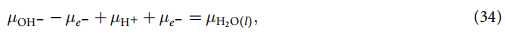
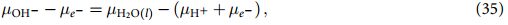
这里，µ_H2O(l) 可根据等式 (30) 计算，(µ_H+ + µ_e- ) 可使用 CHE 方法计算，其中假定平衡为：

使用 RHE 作为参比电极来描述这种平衡，它在氢气压力 p_H2=1bar 和T=298.15 K 的标准条件下工作（但实际实验条件的pH≠0），因此：

电子的剩余电化学势可以表示为：

其中 U_RHE 是电极相对于 RHE 的电位。

结合等式 (36)~(38) ，平衡等式可表示为：

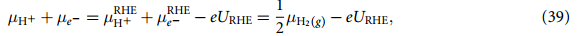
将等式 (39) 代入等式 (35)，最后得出：

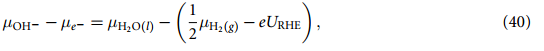
使用在等式(22)至(25)中使用等式(40 )，可以得到

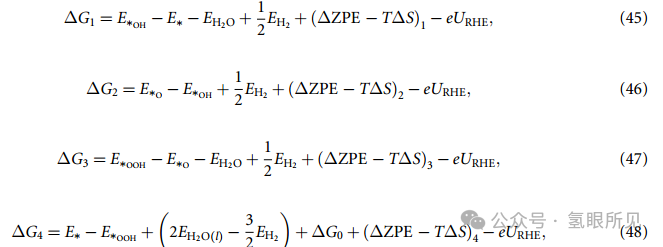
将等式(26 )~( 31)应用到等式(41 )~( 44 )，使用碱性反应机理的反应吉布斯自由能的最终表达式变成：

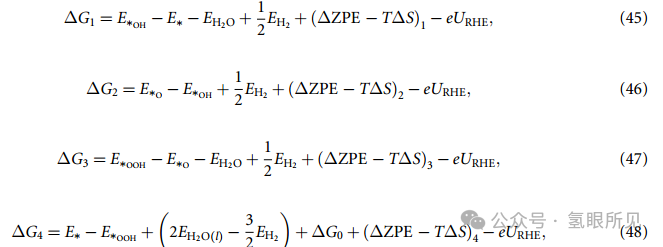
等式(45)~(48)的反应吉布斯自由能遵循求和规则

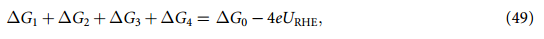
过电势由下式给出：

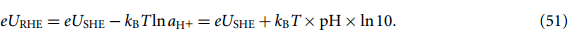
四、酸性和碱性反应机理的比较

在酸性条件下，（H⁺+e^-）的吉布斯自由能与 1/2 H₂ 的吉布斯自由能相关联，反应的吉布斯自由能由等式 (6)~(9) 计算得出。在碱性条件下，根据等式 (35) 和 (40)，（OH^--e^-）的吉布斯自由能与（H⁺+e^-）的吉布斯自由能相关联。碱性反应机理的反应吉布斯自由能可根据等式 (45)~(48) 计算得出。

比较酸性反应机理（等式 (6)~(9) ）和碱性反应机理（等式 (45)~(48) ）的反应吉布斯自由能，可以看出唯一的区别在于电极电位。在酸性机理中，电极电位与 SHE 有关，而在碱性机理中，电极电位与 RHE 有关。因此，尽管酸性环境下的反应机理等式 (2)~(5) 和碱性环境下的反应机理等式 (18)~(21) 不同，但几乎可以用相同的方程计算反应吉布斯自由能。

用于计算酸性和碱性环境下的过电位的等式(16) 和 (50) 完全相同。由于在酸性和碱性情况下计算吉布斯自由能时使用了两种不同的参考电位（SHE 和 RHE），因此数值结果当然会有所不同。这两个参考电位的电极电位可以根据《材料建模手册：当前和新兴材料-2018版》联系起来：

电解水中碱性和酸性条件下析氧反应(OER)机理对比

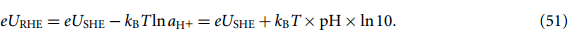
其中 a_H+ 是溶液中 H⁺ 离子的活度。将等式 (51) 代入等式 (45)~(48) 可以得到以 SHE 为基准的反应吉布斯自由能。在 T = 298.15 K 时，k_BT × pH × ln10 ≈ 0.059 × pH eV。

将等式 (51) 代入碱性反应机理的等式 (45)-(48) 中，可以得到与之前文献中酸性反应机理的表达式相同的修正系数 k_BT × pH × ln10。因此，在 pH=0 时，反应吉布斯自由能可根据式（6）~（9）计算，过电势由等式（16）给出。在 pH ≠0 时，反应吉布斯自由能应按 k_BT × pH × ln10 进行修正。或者，使用 RHE 作为参比电极，在任意 pH 值下，反应吉布斯自由能可通过等式 (45)~(48) 计算，过电位可通过等式 (50) 计算。

五、总结

讨论了碱性和酸性条件下的 OER 机理，并推导出两种反应机理的 OER 关键参数，如反应吉布斯自由能和过电势。结果表明，尽管单个反应看起来有很大不同，但只要使用 RHE 作为通用参比，就可以使用相同的方程来计算这些关键参数。讨论了使用不同参比电极（即 RHE 或 SHE）对关键参数方程的影响。研究建议今后在酸性和碱性机制中都使用 RHE 作为参比电极。在这种情况下，等式 (45)~(50) 可用来计算酸性和碱性机理在所有 pH 值下的反应吉布斯自由能和 OER 的过电位。

原文始发于微信公众号（氢眼所见）：电解水中碱性和酸性条件下析氧反应(OER)机理对比

大家好，艾邦氢能源技术网(www.htech360.com)的微信公众号已经开通，主要分享氢燃料电池堆（双极板，质子膜，扩散层，密封胶，催化剂等），储氢罐(碳纤维，环氧树脂，固化剂，缠绕设备，内层塑料及其成型设备，储氢罐，车载供氢系统，阀门)，制氢，加氢，氢燃料汽车动力系统等相关的设备，材料，配件，加工工艺的知识。同时分享相关企业信息。欢迎大家识别二维码，并通过公众号二维码加入微信群和通讯录。