耦合力学和性能模型研究大尺度PEM燃料电池中的非均匀装配效应

前言

在丰田Mirai、本田Clarity等商用燃料电池汽车中，燃料电池堆是核心。它由300多个单体燃料电池单元组成，以获得更高的功率。每个单体燃料电池的结构就像一个三明治，其中膜电极组件（MEA）位于中间，两个双极板（BPs）位于两侧。MEA由气体扩散层（GDL）、微孔层（MPL）、催化剂层（CL）和膜（PEM）组成。大多数的PEM燃料电池堆是通过螺栓组装的，在组装过程中，堆内会出现许多机械行为。BP和GDL之间的接触行为是影响性能的最重要因素之一。适当的接触压力能够减少BP和GDL之间的接触电阻，减少欧姆损失。然而，过高的接触压力会导致GDL的过度压缩，降低孔隙率、渗透率和其他特性，从而阻碍反应气体的传输，增加浓度损失。此外，由于螺栓的布置，BP和GDL的接触压力是不均匀的，导致接触电阻的分布不均匀。因此，研究BP和GDL的接触行为以提高PEM燃料电池的功率密度是非常必要的。

本研究提出了一种耦合力学模型和电池性能模型的方法。本研究开发了一个考虑到真实装配的大尺度全PEM燃料电池有限元力学模型，该模型由螺栓预紧，以研究BP和GDL接触面的接触应力。此外，本研究还开发了一个三维+一维（3D+1D）全PEM燃料电池模型来研究其性能。模型的活化面积为108cm2。在研究中考虑了装配后GDL的非均匀接触电阻、孔隙率和渗透率。将力学有限元模型与性能预测模型相结合，可以为商业电堆的组装和内部机械行为的理解提供指导，这对于优化PEM燃料电池的 "气-液-热-电-力 "管理至关重要。

研究方法

本研究的目标是提出一种方法，将有限元（FEM）模型与大尺度全PEM燃料电池模型结合起来，研究GDL压缩对性能的影响。图1展示了仿真过程。首先，建立一个全面的燃料电池有限元模型，包括几何形状、网格、材料特性、相互作用、边界条件和加载条件。然后，通过这个模型可以得到GDL和BP交界面的接触应力分布以及GDL的变形后体积。之后，可以通过与接触应力和体积有关的经验公式来计算变形后GDL的非均匀接触电阻、孔隙度和渗透率。这些参数可以与3D+1D全PEM燃料电池性能模型相结合。

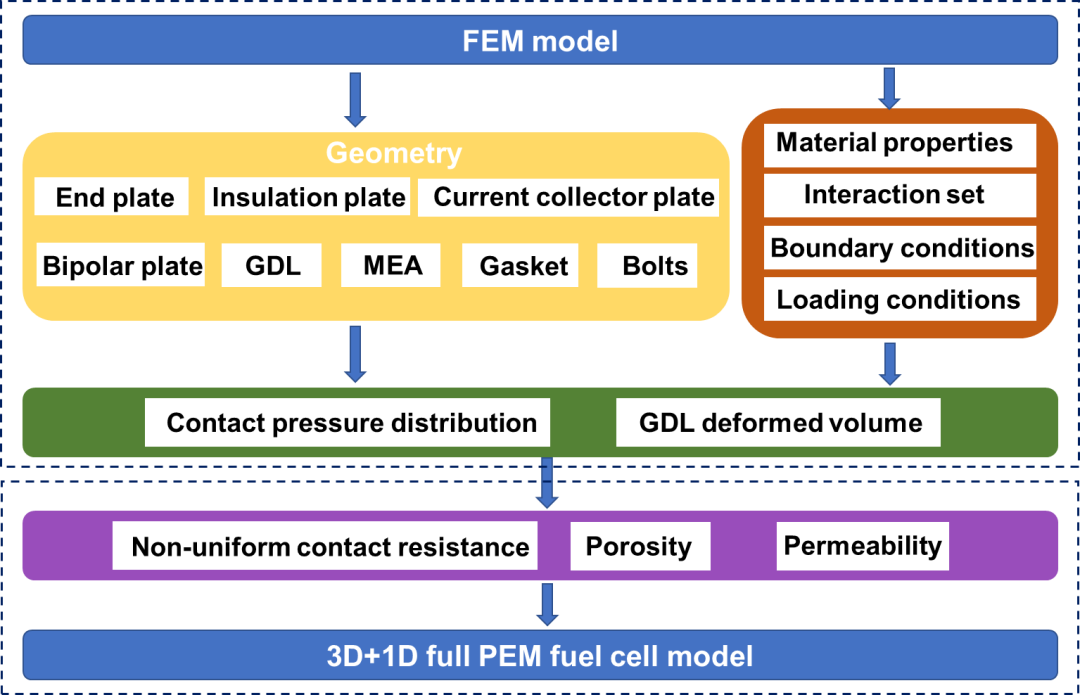
图1 仿真过程示意图

图2展示了燃料电池力学有限元模型。图2 (a)是电池的几何结构，由端板、绝缘板、集流板、双极板、气体扩散层、膜电极层、密封垫圈和14个紧固螺栓组成。由于PEM燃料电池在三个方向具有对称性，为简化计算量，我们采用1/8模型进行计算，如图2(b)所示。由于GDL和BP的接触是最重要的，本文对局部网格进行了细化，GDL的网格尺寸是BP的一半，以获得更准确的结果，如图2(c)所示。图2(d)展示了边界条件和加载条件。

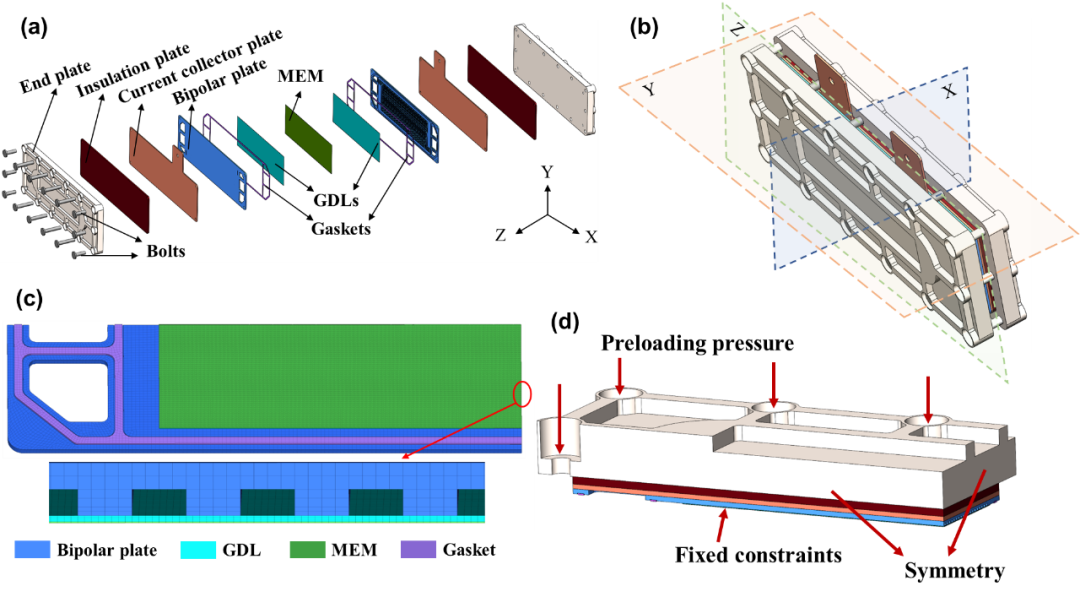
图2 有限元模型几何结构和网格

图3展示了3+1模型的框架和计算域。三维部分包含传统的平行流场，分配区、气体扩散层和阴阳极两侧的扩展层。微孔层、催化剂层和膜被简化为一维部分的计算节点，储存在扩展层中。计算节点被设置在两个相邻部件的界面上。每个扩展层的网格都有一个一维模型，因此三维子模型和一维子模型可以通过扩展层连接。三维子模型中的守恒方程求解的标量值为一维子模型提供边界条件，一维子模型中通量守恒方程求解的标量值被转换为三维子模型的源项，由此三维子和一维子模型进行连接。

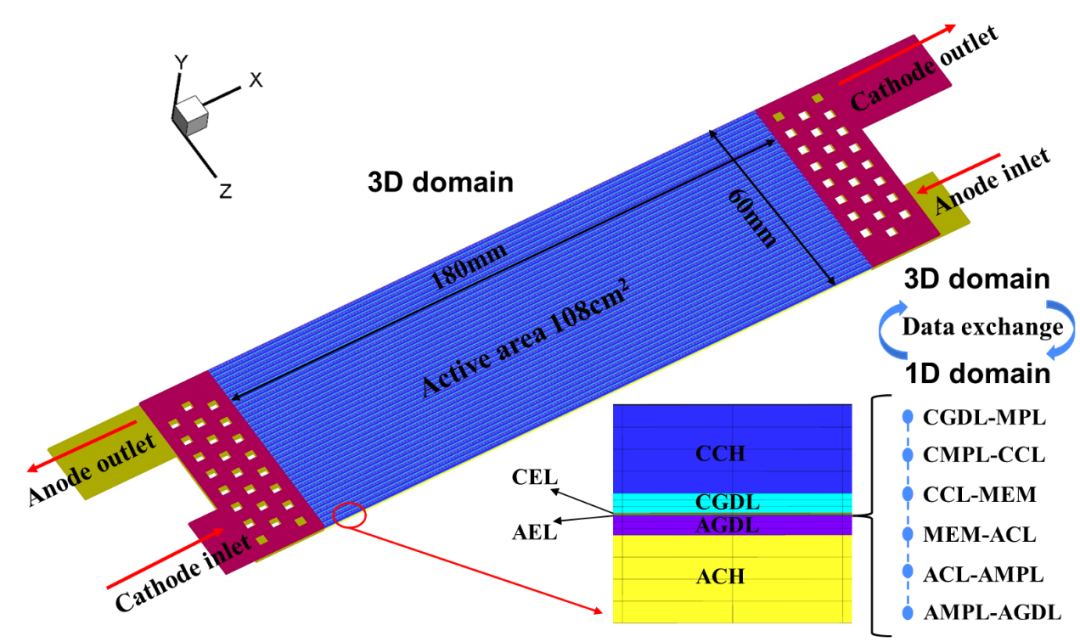
图3 3+1维模型计算域

图4为对有限元模型的实验验证。图4(a)是一个25cm2的小电池，在极板和扩散层之间加入压敏纸，对电池进行装配，得到图4(c)的压敏纸实验结果。对电池结构进行建模，得到图4(b)的仿真结果，为极板和扩散层之间的接触应力分布。可以看出仿真和实验吻合良好。图4(d)是一个108cm2的电池，由14个螺栓组成。同样进行压敏纸实验，图4(f)是实验结果，图4(e)是仿真结果，可以看出仿真同样和实验吻合良好。说明有限元模型的准确性。

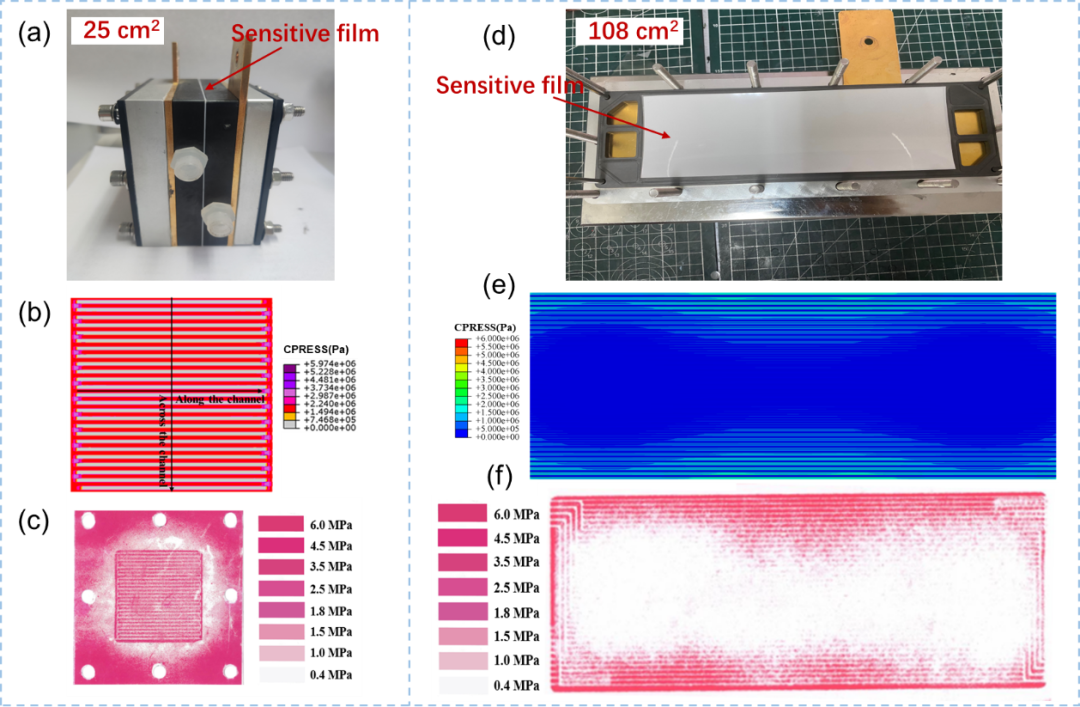
图4 有限元模型实验验证

图5(a)显示了在14个螺栓，每个螺栓3Nm的预紧力下，极板和扩散层的接触应力分布。整体的接触应力数值范围为0MPa到2.62MPa。在流道下面，接触应力是0MPa。在脊下，接触应力随着压缩度的变化而变化。由于螺栓的安排，整体的分布形式展示出中间应力小，四周应力大的趋势。图5(b)表示在跨流道方向应力的变化，可以看到应力的变化非常明显。图5(c)表示沿流道方向的应力变化，呈现两端高中间低的“凹”形趋势。

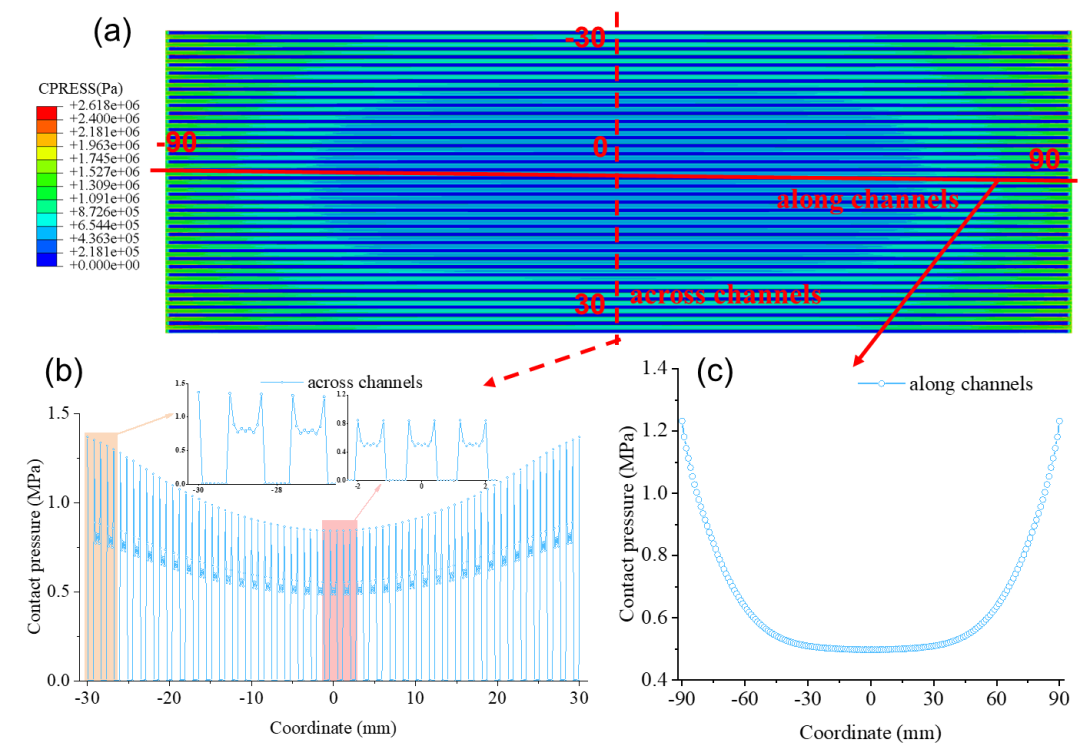
图5 极板和扩散层交界面接触应力分布

不均匀的应力分布会导致不均匀的接触电阻。在获得了GDL上的接触应力分布后，将其通过经验公式转化为接触电阻。GDL被38根流道和37根脊覆盖。因此在每根流道和脊上提取一条数据线，形成了一个75×180的不均匀接触电阻矩阵，耦合进3+1维性能模型中，如图6(a)所示。图6(b)和图6(c)分别展示了对接触电阻不同处理方式的极化曲线和电子欧姆损失。可以看出不考虑接触电阻时电池性能会被明显高估。考虑均匀接触电阻和不均匀接触电阻电池性能相差不大，考虑不均匀的接触电阻时输出电压会略低一些，电子欧姆损失略高一些。

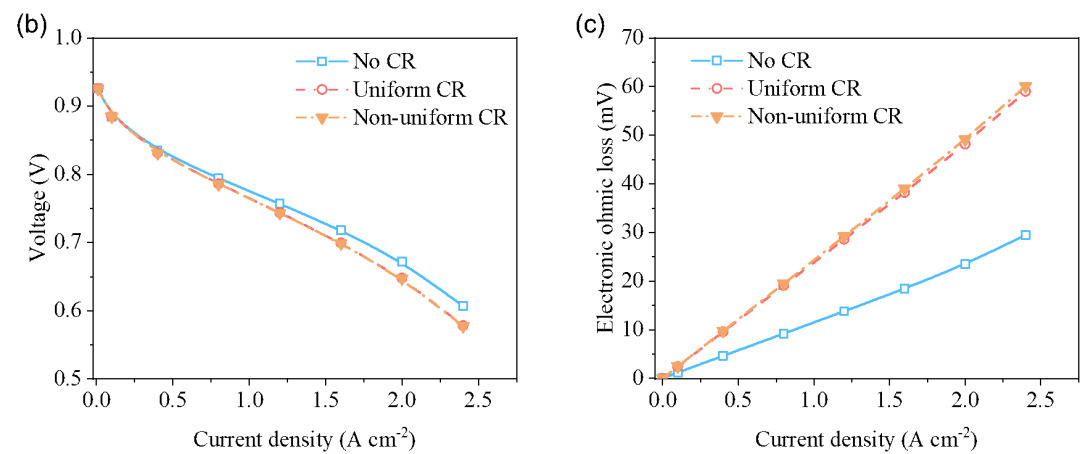
图6 (a)不均匀接触电阻矩阵；(b)三种接触电阻处理方式的极化曲线；(c)三种接触电阻处理方式的电子欧姆损失

图7展示了三种接触电阻处理方式下关键参数的分布，催化层中电流密度、温度和膜态水。可以看出不考虑接触电阻和考虑均匀接触电阻，关键参数的分布相似。当考虑不均匀接触电阻时，在接触应力和接触电阻的分布下，电流密度分布会在入口和四周变高，在中间的电流密度会降低。温度分布同样展示出相同的趋势。膜态水含量的分布整体降低。说明考虑不均匀接触电阻对电池内部关键参数的分布影响较大。

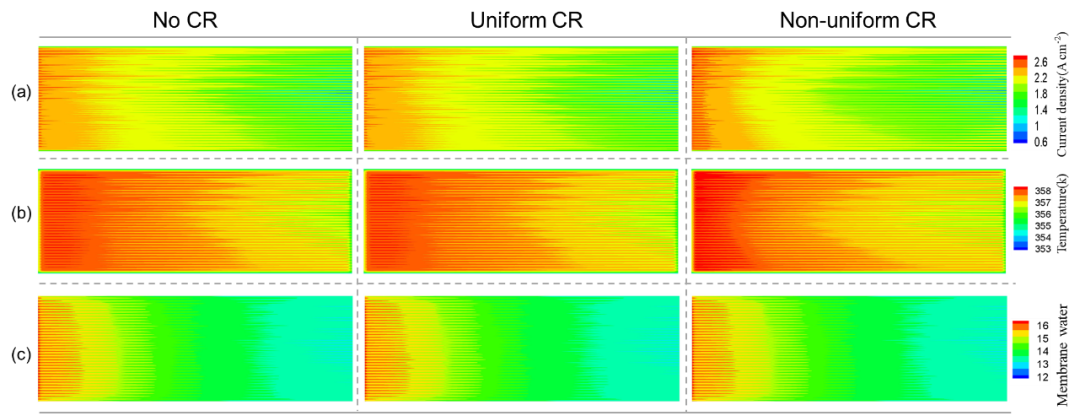
图7 三种接触电阻处理方式下关键参数的分布

此外，本文还考虑了由于装配压缩带来的GDL孔隙度和渗透率的变化。本文研究了从1 Nm到4 Nm七个螺栓预紧力的GDL孔隙度、渗透率和电池性能的变化。图8(a)显示了不同预紧力下GDL压缩后的体积。图8(b)显示了装配后GDL孔隙度的变化，初始孔隙度为0.7。图8(c)显示了装配后GDL渗透率的变化。图8(d)为平均接触应力和接触电阻的变化趋势。

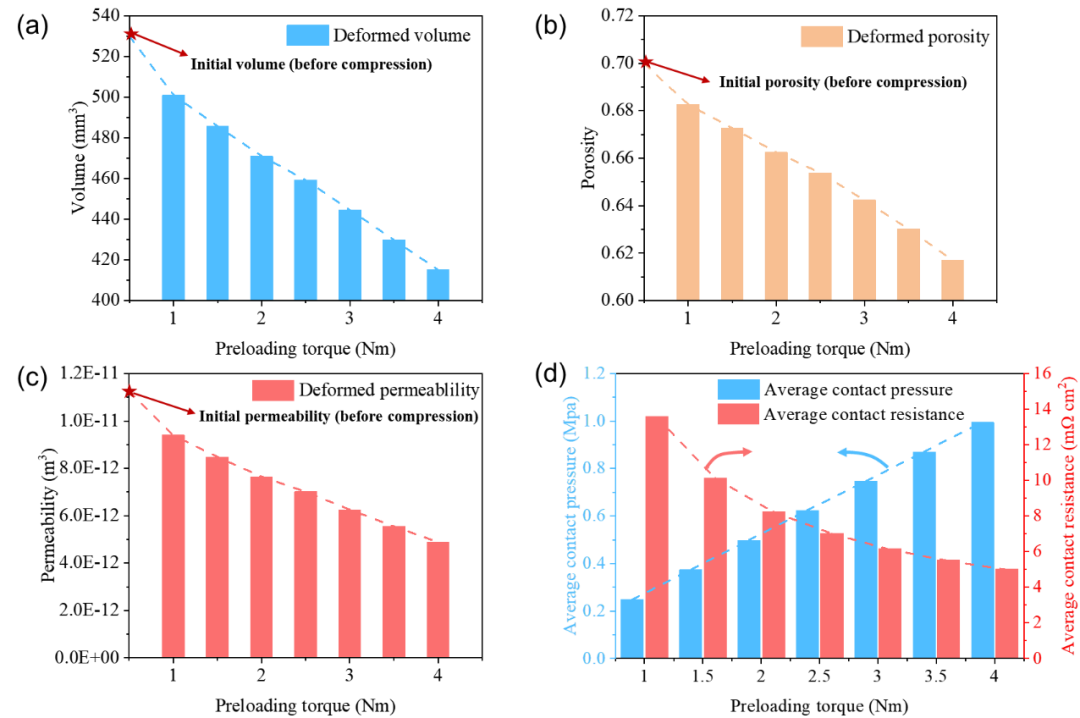
图8 其中螺栓预紧力的GDL体积、孔隙度、渗透率和接触应力、接触电阻的变化

图9显示了七个螺栓预紧力下极化曲线的变化。可以看出在中间欧姆损失段，螺栓预紧力越大，电压越高。这是因为在欧姆损失主导区域，螺栓预紧力越大，接触应力越大，接触电阻越小，电子欧姆损失越小。而在后面传质损失段，由于螺栓预紧力大，压缩量高，孔隙度和渗透率降低，气体传输阻力增大，传质损失上升，电压反而下降。因此最终整体性能是欧姆损失和传质损失互相影响的结果。

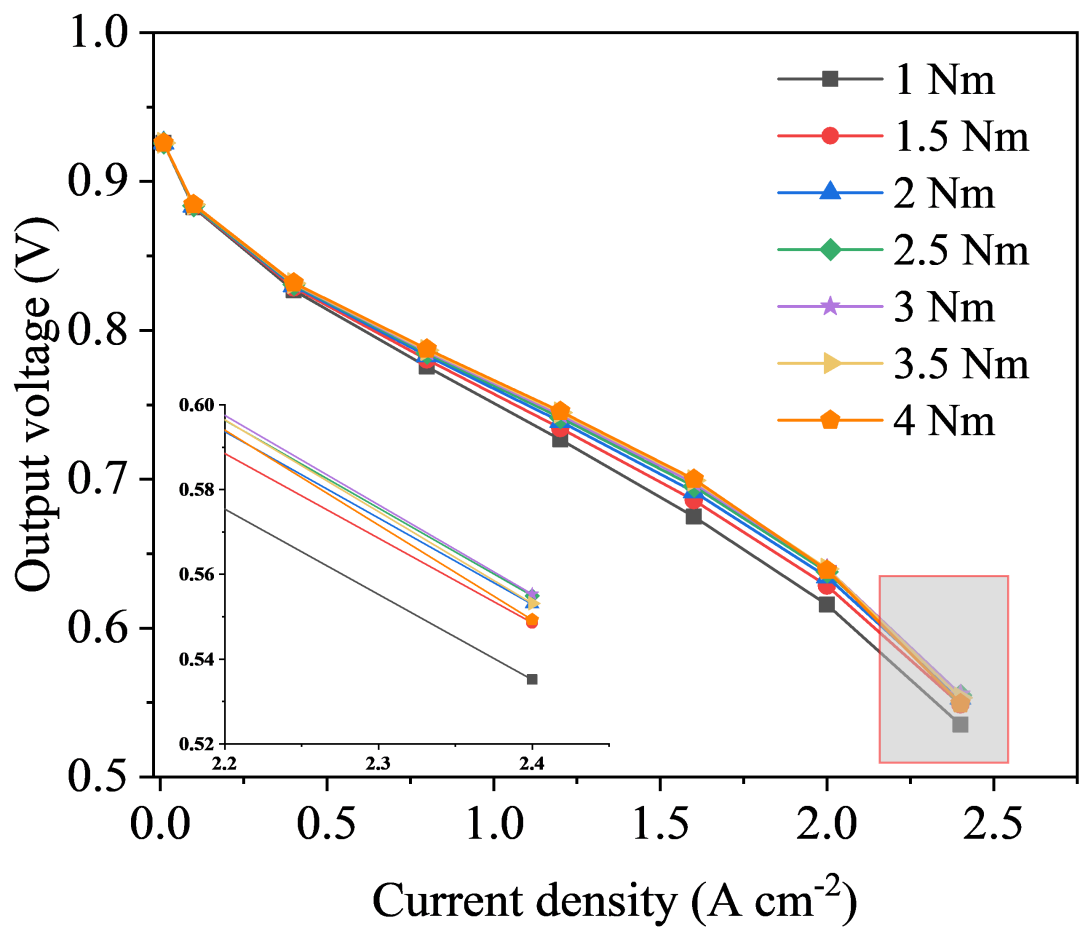
图9 七个预紧力下的极化曲线

作者 | 电化学热物理实验室

原文始发于微信公众号（洁清能源）：耦合力学和性能模型研究大尺度PEM燃料电池中的非均匀装配效应

大家好，艾邦氢能源技术网(www.htech360.com)的微信公众号已经开通，主要分享氢燃料电池堆（双极板，质子膜，扩散层，密封胶，催化剂等），储氢罐(碳纤维，环氧树脂，固化剂，缠绕设备，内层塑料及其成型设备，储氢罐，车载供氢系统，阀门)，制氢，加氢，氢燃料汽车动力系统等相关的设备，材料，配件，加工工艺的知识。同时分享相关企业信息。欢迎大家识别二维码，并通过公众号二维码加入微信群和通讯录。